1.菲涅尔方程:
菲涅耳方程(或称菲涅耳条件)是由法国物理学家奥古斯丁·菲涅耳推导出的一组光学方程,用于描述光在两种不同折射率的介质中传播时的反射和折射。方程中所描述的反射因此还被称作“菲涅耳反射”。
当光线以近法线入射(\(\theta _i \approx \theta_t \approx 0\))时,反射比和透射比分别为:
\(R = R_s = R_p = {(\frac {n_1 – n_2}{n_1 + n_2})}^2\)\(T = T_s = T_p = 1 – R = {\frac {4n_1n_2}{(n_1 + n_2)^2}}\)
对于普通的玻璃,反射比大约为4%。注意窗户对光波的反射包括前面一层以及后面一层,因而少量光波会在两层之间来回振荡形成干涉。如忽略这种干涉效应,这两层合并后的反射比为:\(\frac {2R}{1 + R}\)
2.莫尔条纹:
莫列波纹(英语:Moiré pattern),又译为摩尔纹、莫尔条纹、叠纹、水状波纹,是一种在栅栏状条纹重叠下所产生的干涉影像。
3.Matlab中的数组基本概念:
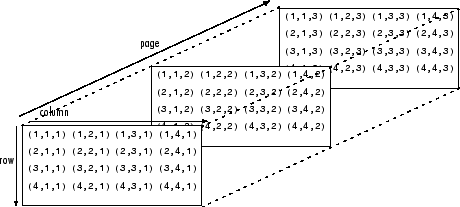
可以通过以下两个下标访问二维矩阵元素:第一个下标表示行索引,第二个下标表示列索引。多维数组使用其他下标进行索引。例如,三维数组使用以下三个下标:
- 第一个下标引用数组维度 1(行)。
- 第二个下标引用维度 2(列)。
- 第三个引用维度 3(页)。上图使用页的概念来表示维度 3 及更高维度。
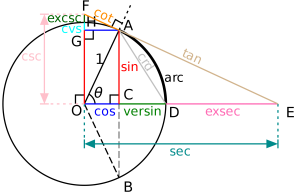
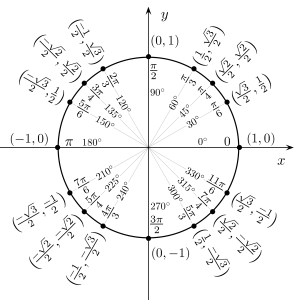
4.三角恒等式:
在数学中,三角恒等式是对出现的所有值都为实变量,涉及到三角函数的等式。这些恒等式在表达式中有些三角函数需要简化的时候是很有用的。一个重要应用是非三角函数的积分:一个常用技巧是首先使用使用三角函数的代换规则,则通过三角恒等式可简化结果的积分。